49ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ
Ζ) Τροχιές πλανητών και δορυφόρων ηλιακού συστήματος σελίδα 2
Λ) Κύκλος και έλλειψη στη Δομή του ατόμου
Λ) Κύκλος και έλλειψη στη Δομή του ατόμου
Ριζωμένοι στο μακρόκοσμό μας αδυνατούμε εύκολα να κατανοήσουμε ένα άλλο κράτος, το κράτος της κβαντομηχανικής, όπου οι γνωστές συμπεριφορές των αντικειμένων καταργούνται. Εκεί όπου τα μικροσκοπικά σωματίδια, όπως είναι τα ηλεκτρόνια, μπορούμε κάποιες φορές να τα θεωρούμε κύματα. Εκεί όπου δεν μπορούμε να προσδιορίσουμε με απόλυτη ακρίβεια και την ταχύτητα και τη θέση τους, αφού σαν πεταλούδες, όσο τα στριμώχνουμε στη γωνία για να βρούμε τη θέση τους, τόσο η ταχύτητά τους γίνεται πιο απροσδιόριστη, με αποτέλεσμα να υπάρχει αβεβαιότητα. Αυτό τον ασύλληπτα μικροσκοπικό κόσμο έχουν οι επιστήμονες τα τελευταία χρόνια φωτογραφήσει με μια καινούργια τεχνική της Μικροσκοπικής Σάρωσης Σήραγγας. Στην παρακάτω φωτογραφία απεικονίζονται τα κύματα των ηλεκτρονίων ατόμων σιδήρου, διατεταγμένων κυκλικά, σε χάλκινη επιφάνεια.

Τον 5°
π.Χ. αιώνα οι Έλληνες φιλόσοφοι Δημόκριτος και Λεύκιππος, διατύπωσαν την άποψη
ότι η ύλη αποτελείται από πολύ μικρά σωματίδια που δεν μπορούν να διαιρεθούν σε
άλλα απλούστερα. Τα σωματίδια αυτά ονόμασαν ατόμους (άτομα).
Να σημειωθεί ότι η άποψη αυτή ήταν αντίθετη με τη θεώρηση του Πλάτωνα και του
Αριστοτέλη για τη συνεχή διαίρεση της ύλης.
Ωστόσο, τα άτομα του Δημόκριτου ξεχάστηκαν για τα επόμενα 2000 χρόνια, μέχρις
ότου στις αρχές του 19ου αιώνα ο Άγγλος χημικός
Dalton
διατυπώσει την ατομική
θεωρία. Σύμφωνα
με την ατομική θεωρία, που αποτελεί θεμέλιο λίθο στην ανάπτυξη της χημείας, οι
δομικές μονάδες της ύλης είναι τα άτομα και τα μόρια (συγκροτήματα ατόμων).
Βέβαια ο
Dalton
δεν μπόρεσε να ερμηνεύσει τη συνένωση ατόμων ίδιου στοιχείου προς σχηματισμό
μορίων. Αυτό ξεκαθαρίστηκε αργότερα (1811) από τον Ιταλό
Avogadro.
Επίσης, τα άτομα του
Dalton
ήταν συμπαγή και αδιαίρετα, άποψη που ήρθε σε αντίθεση με την ανακάλυψη των
πρωτονίων, ηλεκτρονίων και νετρονίων (υποατομικά σωματίδια).


Με την
ανακάλυψη των υποατομικών σωματιδίων άνοιξε ο δρόμος για τη διατύπωση νέων
θεωριών. Οι πιο χαρακτηριστικές απ' αυτές, με επιγραμματική παρουσίαση της
προσφοράς τους στη διαμόρφωση της γνώσης για τη συγκρότηση του ατόμου, είναι:
1.
Rutherford (1911):
η μάζα του ατόμου είναι συγκεντρωμένη σ' ένα πολύ μικρό χώρο που λέγεται πυρήνας.
2.
Bohr (1913):
τα ηλεκτρόνια κινούνται σε καθορισμένες κυκλικές τροχιές γύρω από τον πυρήνα,
που ονομάζονται στιβάδες.
Το ατομικό πρότυπο του αποτελεί συνέχεια του ατομικού πλανητικού προτύπου του Rutherford, στο οποίο ο Bohr ενσωμάτωσε τις πρωτοποριακές για εκείνη την εποχή ιδέες της κβαντικής θεωρίας. Το ατομικό πρότυπο του Bohr μπορεί να περιγραφεί συνοπτικά με τις περίφημες δύο συνθήκες του:
![]() 1η συνθήκη (μηχανική συνθήκη)
1η συνθήκη (μηχανική συνθήκη)
Τα ηλεκτρόνια περιστρέφονται γύρω από τον πυρήνα σε ορισμένες κυκλικές τροχιές. Κάθε επιτρεπόμενη τροχιά έχει καθορισμένη ενέργεια, είναι δηλαδή κβαντισμένη.
![]() 2η συνθήκη
(οπτική συνθήκη)
2η συνθήκη
(οπτική συνθήκη)
Το ηλεκτρόνιο εκπέμπει ενέργεια υπό μορφή ακτινοβολίας μόνο όταν μεταπηδά από μια τροχιά σε μια άλλη, όταν δηλαδή αλλάζει ενεργειακή στάθμη.
Ειδικότερα, όταν ένα ηλεκτρόνιο μεταπίπτει από υψηλότερη σε χαμηλότερη ενεργειακή στάθμη τότε εκπέμπει ακτινοβολία, ενώ όταν μεταπίπτει από χαμηλότερη σε υψηλότερη ενεργειακή στάθμη τότε απορροφά ενέργεια.
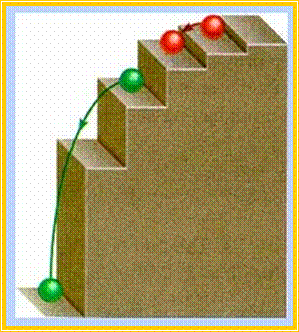
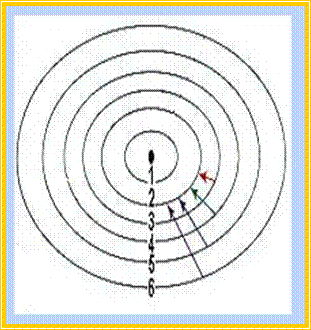
Μηχανικό ανάλογο των αντιλήψεων του
Bohr.Το
e-κινείται
σε ορισμένες τροχιές με καθορισμένες ενεργειακές στάθμες. Όταν το
e- μετακινείται
από τη μια ενεργειακή στάθμη στην άλλη, τότε αποβάλλει ή προσλαμβάνει ενέργεια.
Η παραμονή του ηλεκτρονίου στη διεγερμένη κατάσταση διαρκεί ελάχιστα. Το άτομο
μεταπίπτει σε μια λιγότερη διεγερμένη κατάσταση ή στη θεμελιώδη του κατάσταση.
Κάθε μετάπτωση συνοδεύεται από την εκπομπή ενός φωτονίου.
3.
Sommerfield (1916):
τα ηλεκτρόνια διαγράφουν εκτός από κυκλικές τροχιές (στιβάδες), και ελλειπτικές
(υποστιβάδες).
4.
Σύγχρονες αντιλήψεις για τη
δομή των ατόμων: το
ηλεκτρόνιο συμπεριφέρεται ως κύμα, συνεπώς δεν μπορούμε με ακρίβεια να
γνωρίζουμε την τροχιά που διαγράφει. Εισαγωγή της έννοιας του ατομικού
τροχιακού, του χώρου γύρω από τον πυρήνα όπου έχει μεγάλη πιθανότητα να βρεθεί
ένα ηλεκτρόνιο.
Σε απλές γραμμές έχει διαμορφωθεί η εξής εικόνα για το άτομο. Η μάζα του ατόμου είναι συγκεντρωμένη σ' ένα χώρο που ονομάζεται πυρήνας. Ο πυρήνας συγκροτείται από πρωτόνια (p), που φέρουν θετικό ηλεκτρικό φορτίο, και από ουδέτερα νετρόνια (n). Γύρω από τον πυρήνα και σε σχετικά μεγάλες αποστάσεις απ' αυτόν, κινούνται τα ηλεκτρόνια (e), που φέρουν αρνητικό ηλεκτρικό φορτίο και ευθύνονται για τη χημική συμπεριφορά των ατόμων. Τα άτομα είναι ηλεκτρικά ουδέτερα, καθώς τα πρωτόνια και τα ηλεκτρόνια έχουν αντίθετο στοιχειώδες ηλεκτρικό φορτίο και ο αριθμός των πρωτονίων είναι ίσος με τον αριθμό των ηλεκτρονίων.
Τη βάση για την ανάπτυξή των σύγχρονων αντιλήψεων γύρω από το άτομο έδωσε η κυματική θεωρία της ύλης του De Broglie (1924):
![]() Το φως,
του οποίου το κβάντο ονομάζεται φωτόνιο, όπως και κάθε κινούμενο μικρό σωματίδιο
π.χ. ηλεκτρόνιο, παρουσιάζει διττή φύση, σωματιδίου(κβάντα) και κύματος (ηλεκτρομαγνητικό
κύμα) .
Το φως,
του οποίου το κβάντο ονομάζεται φωτόνιο, όπως και κάθε κινούμενο μικρό σωματίδιο
π.χ. ηλεκτρόνιο, παρουσιάζει διττή φύση, σωματιδίου(κβάντα) και κύματος (ηλεκτρομαγνητικό
κύμα) .

Βέβαια
θα πρέπει να διευκρινίσουμε, ότι η φύση του φωτός (ή ηλεκτρονίου) είναι μία,
δηλαδή, δεν αλλάζει συνεχώς, απλώς, άλλοτε εκδηλώνεται ο σωματιδιακός και άλλοτε
ο κυματικός χαρακτήρας του, ανάλογα με τις πειραματικές συνθήκες που
εφαρμόζουμε. Για παράδειγμα η σωματιδιακή φύση των ηλεκτρονίων εκδηλώνεται με
την περίθλαση των ηλεκτρονίων σε κρυσταλλικό πλέγμα, η οποία βρίσκει εφαρμογή
στη λειτουργία των ηλεκτρονικών μικροσκοπίων.
Το μήκος κύματος, λ,
ενός σωματιδίου μάζας, m,
και ταχύτητας, u,
δίνεται από τη σχέση:
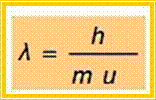
Από την
παραπάνω σχέση προκύπτει ότι για να εκδηλωθεί ο κυματικός χαρακτήρας ενός
σωματιδίου θα πρέπει αυτό να έχει μικρή μάζα και μεγάλη ταχύτητα. Π.χ. μπάλα του
τένις, κινούμενη με ταχύτητα 65
km
h-1 αντιστοιχεί
σε υλικό μήκους κύματος λ -33
m,
το οποίο υπολείπεται κατά πολύ ακόμη και της διαμέτρου των ατομικών πυρήνων.
Αντίθετα, η πολύ μικρή μάζα και η σχετικά μεγάλη ταχύτητα των ηλεκτρονίων μας
επιτρέπουν να ανιχνεύσουμε την κυματική φύση της κίνησης τους (λ ≈
10-10 m).
Θεμελιώδης επίσης συμβολή στην ανάπτυξη της σύγχρονης αντίληψης για το
άτομο έδωσε η
αρχή της αβεβαιότητας (απροσδιοριστίας) του
Heisenberg (1927):
![]() Είναι
αδύνατο να προσδιορίσουμε με ακρίβεια συγχρόνως τη θέση και την ορμή (p=
m
u)
ενός μικρού σωματιδίου π.χ. ηλεκτρονίου.
Είναι
αδύνατο να προσδιορίσουμε με ακρίβεια συγχρόνως τη θέση και την ορμή (p=
m
u)
ενός μικρού σωματιδίου π.χ. ηλεκτρονίου.
Δηλαδή, όσο μεγαλύτερη είναι η ακρίβεια για τον προσδιορισμό της θέσης του σωματιδίου (π.χ. ηλεκτρονίου), τόσο μεγαλύτερο είναι το σφάλμα, δηλαδή, τόσο μεγαλύτερη αβεβαιότητα υπάρχει κατά τον προσδιορισμό της ορμής του, και αντιστρόφως. Στην περίπτωση μεγάλων σωμάτων, π.χ. κινούμενη μπάλα ποδοσφαίρου, τα σφάλματα αυτά είναι αμελητέα. Έτσι, μπορεί να προσδιοριστεί με ακρίβεια ταυτόχρονα η θέση και η ταχύτητα της μπάλας, οποιαδήποτε χρονική στιγμή. Στην περίπτωση, όμως, υποατομικών π.χ. ηλεκτρονίων τα σφάλματα αυτά δεν μπορούν να θεωρηθούν αμελητέα και κατά συνέπεια σωματιδίων υπάρχει πάντοτε κάποια αβεβαιότητα, είτε ως προς τη θέση, είτε ως προς την ορμή τους. Η αποδοχή της αρχής της αβεβαιότητας οδηγεί αυτομάτως στην κατάρριψη όλων των πλανητικών προτύπων, συμπεριλαμβανομένου και του ατομικού πρότυπου Bohr. Πράγματι η παραδοχή της κίνησης του ηλεκτρονίου σε καθορισμένη κυκλική τροχιά προϋποθέτει, με βάση τους νόμους της κυκλικής κίνησης, επακριβή γνώση της θέσης και της ταχύτητας.
Την ίδια εποχή ο Schrödinger έδωσε την περίφημη κυματική εξίσωση, η οποία μαθηματικά συσχετίζει τη σωματιδιακή και κυματική συμπεριφορά του ηλεκτρονίου. Εδώ ανοίγει ο δρόμος για την ανάπτυξη της κβαντομηχανικής, μιας νέας μηχανικής που μπορεί να εφαρμοστεί στο μικρόκοσμο του ατόμου. Σήμερα δε θεωρούμε πλέον ότι ένα ηλεκτρόνιο κινείται σε μια ορισμένη τροχιά γύρω από τον πυρήνα. Στην κβαντομηχανική δε μιλάμε για τη θέση ενός ηλεκτρονίου, αλλά για την πιθανότητα να βρίσκεται σε μια ορισμένη θέση ένα ηλεκτρόνιο.

Με βάση την εξίσωση
Schrödinger
υπολογίζεται η ενέργεια, Εn,
του ηλεκτρονίου, η οποία βρίσκεται σε πλήρη ταύτιση με αυτή που προσδιόρισε ο
Bohr
(κβάντωση ενέργειας). Επιπλέον η εξίσωση προσδιορίζει την πιθανότητα εύρεσης του
ηλεκτρονίου σε ορισμένο χώρο, πράγμα που βρίσκεται σε πλήρη αντίθεση με τις
αντιλήψεις του
Bohr
(καθορισμένες τροχιές). Πιο αναλυτικά, η επίλυση της εξίσωσης
Schrödinger
οδηγεί στις κυματοσυναρτήσεις
ψ,
οι οποίες περιγράφουν την κατάσταση του ηλεκτρονίου με ορισμένη ενέργεια (Εn)
και ονομάζονται ατομικά
τροχιακά.
Η ονομασία
αυτή δόθηκε για να τιμηθεί η προσφορά του
Bohr.
Τα ατομικά τροχιακά αποτελούν συναρτήσεις θέσης του ηλεκτρονίου στο άτομο π.χ.
είναι της μορφής ψ(x,
y,
z),
όπου
x,
y,
z
είναι οι συντεταγμένες που καθορίζουν τη θέση του ηλεκτρονίου γύρω από τον
πυρήνα. Το ψ αυτό
καθεαυτό δεν έχει φυσική σημασία. Βέβαια, αποτελεί κατά κάποιο τρόπο μια ένδειξη
της παρουσίας, ή μη, του ηλεκτρονίου γύρω από τον πυρήνα (ψ =0
υποδηλώνει την απουσία και ψ ≠0
την παρουσία του ηλεκτρονίου). Αντίθετα, το ψ2 έχει
σημαντική φυσική σημασία, καθώς
![]() το ψ2 εκφράζει
την πιθανότητα να βρεθεί το ηλεκτρόνιο σε ένα ορισμένο σημείο του χώρου γύρω από
τον πυρήνα.
το ψ2 εκφράζει
την πιθανότητα να βρεθεί το ηλεκτρόνιο σε ένα ορισμένο σημείο του χώρου γύρω από
τον πυρήνα.
![]() Το ψ2 (ή
ακριβέστερα το –eψ2,
όπου –e
το φορτίο του ηλεκτρονίου) εκφράζει την κατανομή ή την πυκνότητα του
ηλεκτρονιακού νέφους στο χώρο γύρω από τον πυρήνα.
Το ψ2 (ή
ακριβέστερα το –eψ2,
όπου –e
το φορτίο του ηλεκτρονίου) εκφράζει την κατανομή ή την πυκνότητα του
ηλεκτρονιακού νέφους στο χώρο γύρω από τον πυρήνα.
Εδώ θα πρέπει να παρατηρήσουμε, ότι η εξίσωση Schrödinger διατυπώθηκε για να περιγράψει μαθηματικά τη συμπεριφορά του ηλεκτρόνιου του ατόμου του υδρογόνου. Μπορεί βέβαια με κατάλληλες προσεγγίσεις να εφαρμοστεί και σε πολυηλεκτρονικά άτομα, παρόλο που η επίλυση της εξίσωσης και ο προσδιορισμός των κυματοσυναρτήσεων, ψ, για τα ηλεκτρόνια σ’ αυτές τις περιπτώσεις είναι ένα πολύπλοκο μαθηματικό πρόβλημα. Ωστόσο, τα συμπεράσματα που προκύπτουν από το υδρογόνο, μπορούν να αποτελέσουν τη βάση για να μελετήσουμε την ηλεκτρονιακή δομή βαρύτερων ατόμων.
Παρακάτω δίνεται υπό μορφή παραδείγματος, η σχηματική απεικόνιση του ηλεκτρονιακού νέφους (της συνάρτησης ψ2) του ατόμου του υδρογόνου, στη θεμελιώδη του κατάσταση.
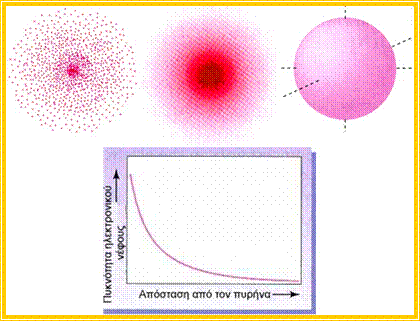
Σχηματική
απεικόνιση της πυκνότητας του ηλεκτρονιακού νέφους του ατόμου του υδρογόνου σε
μη διεγερμένη κατάσταση: α) με «στιγμές» β) με πυκνότητα χρώματος γ) με
«οριακές» καμπύλες (πάνω).
Γραφική παράσταση της πυκνότητας του ηλεκτρονιακού νέφους σε συνάρτηση με την
απόσταση από τον πυρήνα (κάτω).
Οι παραπάνω γραφικές παραστάσεις απεικονίζουν την πυκνότητα του ηλεκτρονιακού νέφους ( ψ2 ) και όχι το τροχιακό (ψ), όπως πολλές φορές αναφέρεται (χάριν απλούστευσης).
Οι τέσσερις κβαντικοί αριθμοί που περιγράφουν πλήρως την κατάσταση του ηλεκτρονίου στο άτομο είναι οι (n, l, ml, ms ) και προσδιορίζουν, αντίστοιχα
v τη στιβάδα (φλοιό)
v την υποστιβάδα (υποφλοιό)
v το τροχιακό και
v το spin του ηλεκτρονίου
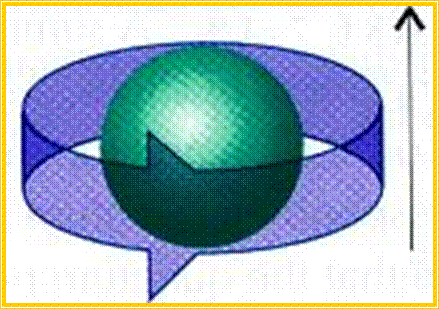
Το ηλεκτρόνιο μπορεί να κινηθεί γύρω από τον άξονα του (spin ηλεκτρονίου), είτε με τη φορά των δεικτών του ρολογιού, είτε αντίστροφα. Στην πρώτη περίπτωση έχουμε ms = - ½ και στη δεύτερη περίπτωση ms = + ½ .
Γραφική απεικόνιση ατομικών τροχιακών
Η
απεικόνιση των ατομικών τροχιακών ή ακριβέστερα της πυκνότητας του ηλεκτρονιακού
νέφους μπορεί να γίνει με πολλούς τρόπους. Η παράσταση των τροχιακών
(συναρτήσεων ψ2)
με οριακές καμπύλες είναι από τις πιο συνηθισμένες. Το περίγραμμα της καμπύλης
περικλείει το 90-99% της πυκνότητας του ηλεκτρονιακού νέφους.
Τα
s
τροχιακά (l =
0) έχουν σφαιρική συμμετρία, που σημαίνει ότι η πιθανότητα να βρεθεί το
ηλεκτρόνιο σε μια ορισμένη απόσταση από τον πυρήνα είναι ανεξάρτητη από την
κατεύθυνση. Τα
s
τροχιακά συμβολίζονται με σφαίρες, το μέγεθος των οποίων εξαρτάται από τον κύριο
κβαντικό αριθμό. Όσο μεγαλύτερος είναι ο κύριος κβαντικός αριθμός n,
στον οποίο ανήκει το τροχιακό s,
τόσο μεγαλύτερη είναι και η ακτίνα της σφαίρας.
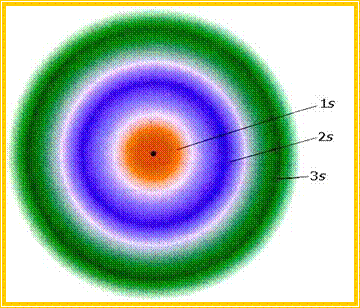
Σχηματική παρουσίαση των 1s, 2s και 3s τροχιακών (συναρτήσεων ψs2). Η ένταση του χρώματος είναι ανάλογη προς την πυκνότητα του ηλεκτρονιακού νέφους.
Με ανάλογη σκέψη, τα p τροχιακά
έχουν το σχήμα διπλού λοβού. Το σχήμα του λοβού είναι το σχήμα που προκύπτει αν
ένα σφαιρικό μπαλόνι «τραβηχτεί» από κάποιο σημείο του, π.χ. από εκεί που είναι
δεμένο. Να παρατηρήσουμε επίσης ότι το ηλεκτρόνιο στο p τροχιακό,
αντίθετα από ότι συμβαίνει στο s, έχει ελάχιστη
πιθανότητα να βρεθεί κοντά στον πυρήνα.
Όπως γνωρίζουμε, σε κάθε τιμή του κύριου κβαντικού αριθμού με n >=
2, αντιστοιχούν τρία p τροχιακά, που έχουν ίδιο
μέγεθος και σχήμα αλλά διαφορετικό προσανατολισμό. Το καθένα απ’ αυτά τα
τροχιακά, px, py και pz,
προσανατολίζεται στον αντίστοιχο άξονα, x,
y και z. Επίσης, όπως και
στην περίπτωση των s, το μέγεθος του p τροχιακού
καθορίζεται από την τιμή του κύριου κβαντικού αριθμού. Δηλαδή, όσο μεγαλύτερος
είναι ο κύριος κβαντικός αριθμός n στον οποίο
ανήκει το τροχιακό p, τόσο μεγαλύτερο είναι το
μέγεθος του τροχιακού.
Τέλος, τα d τροχιακά (l =
2) είναι πέντε (ml: -2, -2, 0, +1,
+2) με σχετικά πολύπλοκη απεικόνιση. Το ίδιο ισχύει και για τα f τροχιακά
(l = 3) που είναι
συνολικά 7 (ml: -3, -2, -2, 0, +1,
+2, +3).
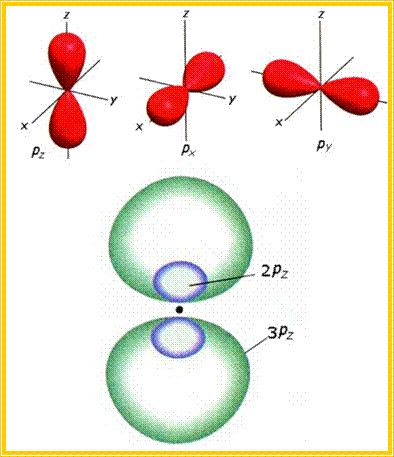
Σχηματική
παρουσίαση των τριών p τροχιακών, px, py και pz (συναρτήσεων ψp2)
β. Σχετικά μεγέθη των τροχιακών 2pz και
3pz.
Τα τροχιακά p έχουν
σχήμα παρόμοιο με τα «βαράκια» της γυμναστικής.