49^ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ

• Α) Ο Κύκλος στην Καθημερινότητα                                                                                                                                                   

• Β) Κύκλος ζωής                                                                                                                                                                                  

• Γ) Τα μεγαλιθικά κυκλικά μνημεία                                                                                                                                                  

• Δ) Τα κυκλικά μοτίβα και οι εικόνες αφθονούν στα λαϊκά πολιτισμικά έθιμα                                                                                                                    

• Ε) Ο χορός και η παράδοση                                                                                                                                                                 

• Ζ) Η οικογένεια και η παράδοση                                                                                                                                                         

• Η) Κοσμογονικοί Μύθοι και Θεωρίες για τον  κύκλο                                                                                                                                                          

• Θ) Ορθοδοξία και κύκλος                                                                                                                                                                    

• Ι)  Εικονογραφικός κύκλος                                                                                                                                                                                                

• Κ) Κύκλος του νερού                                                                                                                                                        

• Λ) Μαθηματικά και κύκλος                                                                                                                                                           

• Μ) Κωνική τομή                                                                                                                                                                                  

• Ν) Αστρονομία και κύκλος

Λ) Μαθηματικά και κύκλος

Μέσα από την καθημερινή ζωή μπορούμε να βρούμε αρκετά παραδείγματα καμπυλών. Όπως π.χ. ο ήλιος στη δύση του, ο τροχός ενός ποδηλάτου η στεφάνη της μπασκέτας, ένα μεταλλικό νόμισμα, το ρολόι μας, μια τούρτα γενεθλίων, ένας δίσκος μουσικής κλπ.

Το πρώτο σχήμα που μπορούσε να επινοήσει ή να ανακαλύψει στη γη ο άνθρωπος είναι φυσικά, ο κύκλος. Ο ήλιος και το φεγγάρι αρκούν για να δώσουν στο μάτι το σχήμα και στην ψυχή την ομορφιά της τελειότητας. Και όταν φθάσει η ώρα της σκέψης, τότε η Γεωμετρία αποκτά το πιο πολύτιμο σχήμα της.

Ø  Κύκλος λέγεται το σύνολο όλων των σημείων του επιπέδου που απέχουν την ίδια απόσταση από ένα σταθερό σημείο Ο.

     Η απόσταση αυτή συμβολίζεται με ρ και λέγεται ακτίνα του κύκλου. Το σημείο  Ο λέγεται κέντρο του κύκλου.

    Ένας κύκλος με κέντρο Ο και ακτίνα ρ, συμβολίζεται με συντομία (Ο, ρ).

    Για να σχεδιάσουμε ένα κύκλο χρησιμοποιούμε το διαβήτη.

    Δύο κύκλοι με ακτίνες ίσες είναι ίσοι.                                 

 Άρα:

	Κύκλος (Ο,ρ) είναι ο γεωμετρικός τόπος των σημείων Μ του επιπέδου για τα οποία ισχύει ΟΜ = ρ
	Κυκλικός δίσκος (Ο, ρ) είναι ο κύκλος (Ο, ρ) μαζί με το μέρος του επιπέδου που περικλείει.
	Όλα τα σημεία του κυκλικού δίσκου απέχουν από το κέντρο Ο απόσταση μικρότερη ή ίση με την ακτίνα ρ.
	Κάθε σημείο Σ του επιπέδου του κύκλου C(Ο,ρ) για το οποίο ισχύει ΣΟ < ρ, λέγεται εσωτερικό σημείο του κύκλου. Αντίστοιχα κάθε σημείο Ν του επιπέδου για το οποίο ΝΟ > ρ λέγεται εξωτερικό σημείο του κύκλου. Το σύνολο των εσωτερικών σημείων του κύκλου ονομάζεται εσωτερικό του κύκλου και ο κύκλος μαζί με το εσωτερικό του λέγεται κυκλικός δίσκος.
	Ένα ευθύγραμμο τμήμα που ενώνει δύο σημεία ενός κύκλου λέγεται χορδή του κύκλου. Όταν αυτή περιέχει το κέντρο του, λέγεται διάμετρος και τα άκρα της χαρακτηρίζονται αντιδιαμετρικά.

  Κατά τον Ευκλείδη (Στοιχεία, βιβλίο πρώτο),

   "Κύκλος εστί σχήμα επίπεδον υπό μιας γραμμής περιεχόμενον [ή καλείται περιφέρεια], πρός ήν αφ'ενός σημείου τών εντός τού σχήματος κειμένων πάσαι αι προσπίπτουσαι ευθείαι [πρός τήν τού κύκλου περιφέρειαν] ίσαι αλλήλαις εισίν. Κέντρον δε τού κύκλου το σημείον καλείται. Διάμετρος δε του κύκλου εστίν ευθεία τις διά τού κέντρου ηγμένη και περατουμένη εφ' εκάτερα τά μέρη υπό τής τού κύκλου περιφερείας, ήτις καί δίχα τέμνει τόν κύκλον".

Ευκλείδης

  Στον παραπάνω ορισμό ο Ευκλείδης ταυτίζει τον κύκλο με τον δίσκο. Για αυτό το λόγο εμφανίζεται ο όρος περιφέρεια.

  Με άλλα λόγια οι λέξεις περιφέρεια και κύκλος περίγραφαν στην αρχαιότητα αυτά που σε σημερινή ορολογία λέμε κύκλος και δίσκος αντίστοιχα.

  Από την τριγωνική ανισότητα, κάθε χορδή σε κύκλο είναι μικρότερη ή ίση της διαμέτρου.

  Εάν  C είναι η περίμετρος του κύκλου, τότε: C = 2πρ,      όπου π=3,14….

  Η διάμετρος δ του κύκλου: δ = 2ρ     όπου ρ η ακτίνα του κύκλου

  Το εμβαδόν του κυκλικού δίσκου δίνεται από τον τύπο: Ε= πρ²

  Ο κύκλος είναι το σχήμα του επιπέδου με το μεγαλύτερο εμβαδόν για δεδομένη περίμετρο.

   Ο Τετραγωνισμός του κύκλου είναι ένα από τα αρχαιότερα γεωμετρικά προβλήματα.   Η διατύπωση του είναι απλή: Ζητείται η κατασκευή με κανόνα και διαβήτη ενός τετραγώνου του οποίου το εμβαδόν να είναι ίσο με το εμβαδόν ενός δοθέντος κύκλου. Το 1882, ο μαθηματικός Φέρντιναντ Φον Λίντεμαν (Ferdinand von Lindemann) απέδειξε το αδύνατο της επίλυσης του προβλήματος.

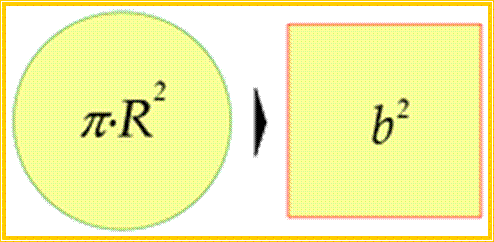
Ο κύκλος και το τετράγωνο του σχήματος έχουν το ίδιο εμβαδόν. Παρόλα αυτά δεν υπάρχει μια γεωμετρική μέθοδος που επιτρέπει να μεταβαίνουμε από το σχήμα στα αριστερά στο σχήμα στα δεξιά.

  Τετραγωνίζω τον κύκλο σημαίνει ότι κατασκευάζω, με γεωμετρική ή αλγεβρική μέθοδο, ένα τετράγωνο με εμβαδόν ίσο με το εμβαδόν του κύκλου.

Η δυσκολία του προβλήματος συνίσταται σε δύο περιορισμούς που έθεσαν σε αυτό οι αρχαίοι Έλληνες μαθηματικοί. Πιο συγκεκριμένα, για να θεωρηθεί αποδεκτή μία λύση του προβλήματος, σε αυτήν θα πρέπει:

v  να χρησιμοποιηθεί μόνο κανόνας και διαβήτης, προκειμένου η απόδειξη να ανάγεται πλήρως στα θεωρήματα του Ευκλείδη, και

v  να μην πραγματοποιείται μετά από άπειρο αριθμό βημάτων.

  Αποδεικνύεται ότι το πρόβλημα του τετραγωνισμού του κύκλου επιλύεται εύκολα αν άρουμε οποιονδήποτε από αυτούς τους δύο περιορισμούς.

  Η επίλυση του προβλήματος συνδέεται άμεσα με την υπερβατικότητα του αριθμού π: Αν κάποιος έχει καταφέρει να τετραγωνίσει τον κύκλο, σημαίνει ότι με κάποιο τρόπο έχει υπολογίσει μία συγκεκριμένη αλγεβρική τιμή για το π. Κάτι τέτοιο όμως δεν είναι εφικτό στην περίπτωση που ο αριθμός π είναι υπερβατικός, οπότε δεν έχει συγκεκριμένη αλγεβρική τιμή. Πράγματι, το ενδιαφέρον για την επίλυση του προβλήματος του τετραγωνισμού του κύκλου εξανεμίζεται το 1882, όταν ο Φέρντιναντ Φον Λίντεμαν (Ferdinand von Lindemann) απέδειξε ότι το π είναι υπερβατικός αριθμός.

  Ο τετραγωνισμός του κύκλου είναι ένα από τα διασημότερα μαθηματικά προβλήματα. Ένα μεγάλο πλήθος μαθηματικών, από την αρχαιότητα μέχρι τα τέλη του 19ου αιώνα, έχουν αφιερώσει μεγάλο κομμάτι της εργασίας τους στην προσπάθεια να τετραγωνίσουν τον κύκλο.

  Αυτό είχε ως αποτέλεσμα η φράση «τετραγωνίζω τον κύκλο» να υιοθετηθεί και από την κουλτούρα των μη μυημένων στα μαθηματικά, ως συνώνυμη του «επιδιώκω το ακατόρθωτο / το καταδικασμένο σε αποτυχία». Στην ελληνική γλώσσα για παράδειγμα, η φράση «σιγά μην τετραγωνίσουμε και τον κύκλο» υποδηλώνει άρνηση συμμετοχής σε μια προσπάθεια που είναι από δύσκολο έως αδύνατο να οδηγήσει σε επιτυχία.