49^ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΑΘΗΝΩΝ

• Α) Ο Κύκλος στην Καθημερινότητα                                                                                                                                                   

• Β) Κύκλος ζωής                                                                                                                                                                                  

• Γ) Τα μεγαλιθικά κυκλικά μνημεία                                                                                                                                                  

• Δ) Τα κυκλικά μοτίβα και οι εικόνες αφθονούν στα λαϊκά πολιτισμικά έθιμα                                                                                                                    

• Ε) Ο χορός και η παράδοση                                                                                                                                                                 

• Ζ) Η οικογένεια και η παράδοση                                                                                                                                                         

• Η) Κοσμογονικοί Μύθοι και Θεωρίες για τον  κύκλο                                                                                                                                                          

• Θ) Ορθοδοξία και κύκλος                                                                                                                                                                    

• Ι)  Εικονογραφικός κύκλος                                                                                                                                                                                                

• Κ) Κύκλος του νερού                                                                                                                                                        

• Λ) Μαθηματικά και κύκλος                                                                                                                                                           

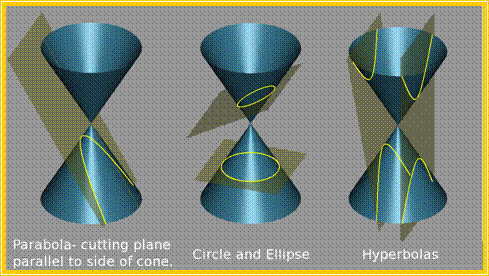
• Μ) Κωνική τομή                                                                                                                                                                                  

• Ν) Αστρονομία και κύκλος

Μ) Κωνική τομή

 Ονομάζεται μία καμπύλη που προκύπτει από την τομή κώνου και επιπέδου, ή ακριβέστερα, από την τομή ενός επιπέδου με δύο ίσες ορθές άπειρες κωνικές επιφάνειες που έχουν κοινό άξονα και συνδέονται στην κορυφή τους (ο ένας κώνος εφαρμόζει "αναποδογυρισμένος" πάνω στην κορυφή του άλλου). Όλες οι καμπύλες το πολύ δεύτερης τάξης στο επίπεδο είναι κωνικές τομές.

Εξίσωση Κύκλου

Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και C ο κύκλος με κέντρο το σημείο O(0,0) και ακτίνα ρ.

Γνωρίζουμε από τη Γεωμετρία ότι ένα σημείο M(x,y) ανήκει στον κύκλο C, αν και μόνο αν απέχει από το κέντρο του Ο απόσταση ίση με ρ, δηλαδή, αν και μόνο αν ισχύει: (ΟΜ)  =ρ (1)

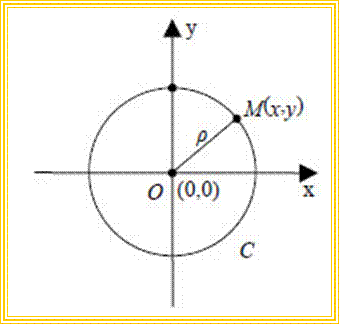
  Άρα, ο κύκλος με κέντρο το σημείο O(0,0) και ακτίνα ρ έχει εξίσωση

Παρατηρούμε, δηλαδή, ότι οι συντεταγμένες των σημείων του κύκλου και μόνο αυτές επαληθεύουν την εξίσωση.

Για παράδειγμα, ο κύκλος με κέντρο το σημείο Ο(0,0) και ακτίνα ρ=1 έχει εξίσωση x² + y² =1 .  Ο κύκλος αυτός λέγεται  μοναδιαίος κύκλος.

Παραμετρικές Εξισώσεις Κύκλου

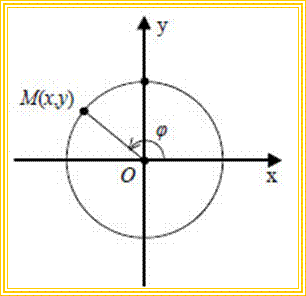
  Οι εξισώσεις αυτές λέγονται παραμετρικές εξισώσεις του κύκλου C.

Εφαπτομένη Κύκλου

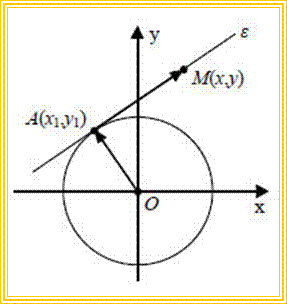
  Έστω ε η εφαπτομένη του κύκλου C: x² + y ² = ρ² σε ένα σημείο του A(x₁,y₁) .    Γνωρίζουμε από τη Γεωμετρία ότι ένα σημείο M(x,y) ανήκει στην ε, αν και μόνο αν

   Η εφαπτομένη του κύκλου x² + y ² = ρ² στο σημείο του A(x₁,y₁) έχει εξίσωση

Η Εξίσωση X² + y² + Ax +By + Γ =0

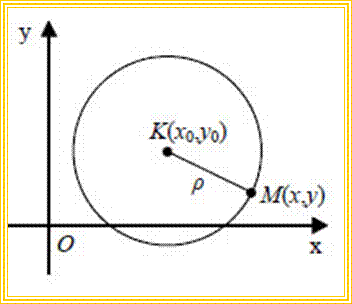
Κάθε κύκλος έχει εξίσωση της μορφής


και αντιστρόφως κάθε εξίσωση της μορφής (Ι) παριστάνει κύκλο.

• Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και C ο κύκλος με κέντρο K(x₀,y₀) και ακτίνα ρ. Ο κύκλος με κέντρο K(x₀,y₀) και ακτίνα ρ έχει εξίσωση: